LeetCode
LeetCode Hot 100
240. 搜索二维矩阵 II - 力扣(LeetCode)
搜索二维矩阵 II 点击展开题目
编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性:
每行的元素从左到右升序排列。 每列的元素从上到下升序排列。
示例 1:
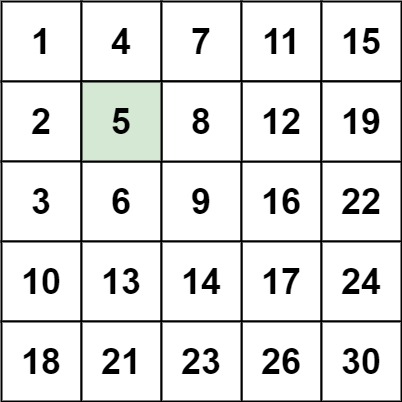
输入:matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5 输出:true 示例 2:
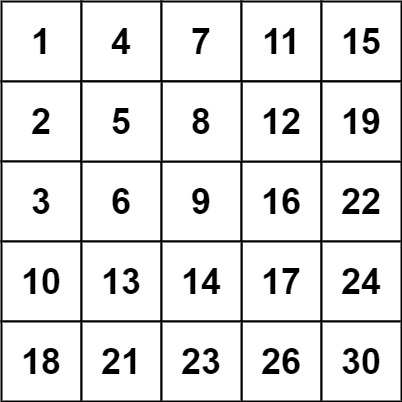
输入:matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20 输出:false
提示:
m == matrix.length n == matrix[i].length 1 <= n, m <= 300 -109 <= matrix[i][j] <= 109 每行的所有元素从左到右升序排列 每列的所有元素从上到下升序排列 -10^9 <= target <= 10^9
思路1:观察到m、n均小于等于300,可以直接双重循环进行枚举。 时间复杂度 O(mn) 空间复杂度 O(1)
class Solution {
public:
bool searchMatrix(vector<vector<int>>& matrix, int target) {
for(int i = 0; i < matrix.size(); i ++)
{
for(int j = 0; j < matrix[0].size(); j ++)
{
if(matrix[i][j] == target)
{
return true;
}
}
}
return false;
}
};思路2:对每一行进行二分查找 时间复杂度 O(mlogn) 空间复杂度 O(1)
class Solution {
public:
bool searchMatrix(vector<vector<int>>& matrix, int target) {
int n = matrix.size();
int m = matrix[0].size();
//枚举每行
for(int i = 0; i < n; i ++)
{
//对每一行进行二分查找
int l = 0, r = m - 1;
while(l <= r)
{
int mid = (r - l) / 2 + l;//直接(l+r)/2可能会溢出
if(matrix[i][mid] > target) r = mid - 1;
else if(matrix[i][mid] < target) l = l + 1;
else return true;
}
}
return false;
}
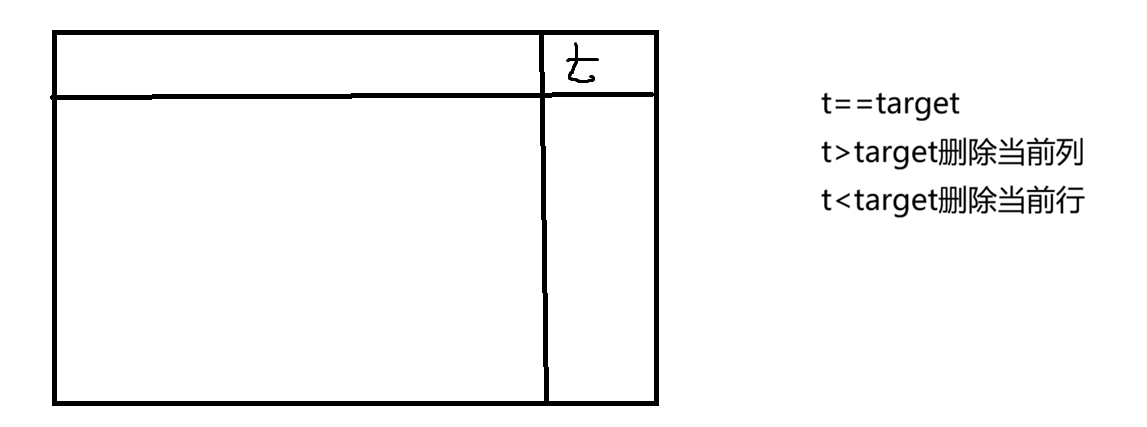
};思路3:从右上角进行查找,设当前的数为t,共有三种可能
- t==target返回true即可
- t>target代表t所在列元素都比target大,答案一定不在当前列,可以删除当前列
- t<taeget代表t所在行元素都比target小,答案一定不在当前行,可以删除当前行
时间复杂度 O(m+n)
空间复杂度 O(1)
class Solution {
public:
bool searchMatrix(vector<vector<int>>& matrix, int target) {
if(matrix.empty() || matrix[0].empty()) return false;
int n = matrix.size();
int m = matrix[0].size();
int i = 0, j = m - 1;
while(i < n && j >= 0)
{
int t = matrix[i][j];
if(t == target) return true;
else if(t > target) j --;
else i ++;
}
return false;
}
};