链表
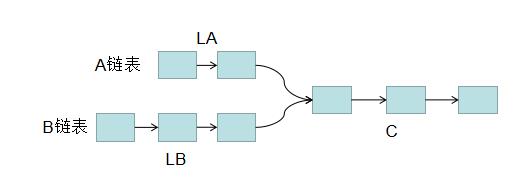
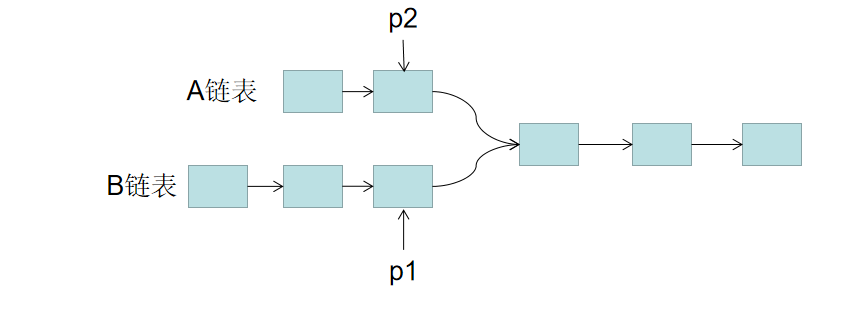
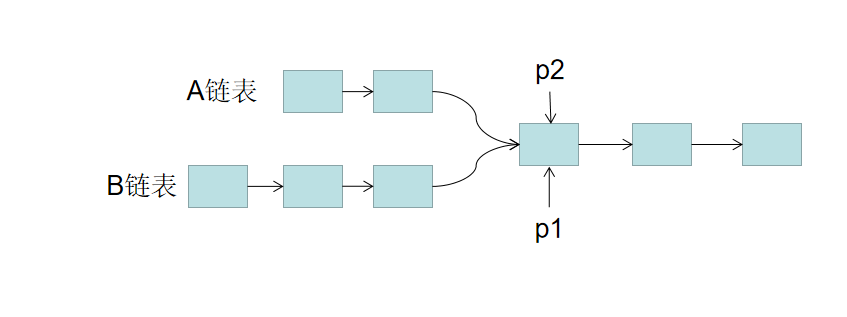
题意:输入两个链表,找出它们的第一个公共结点。 当不存在公共节点时,返回空节点。
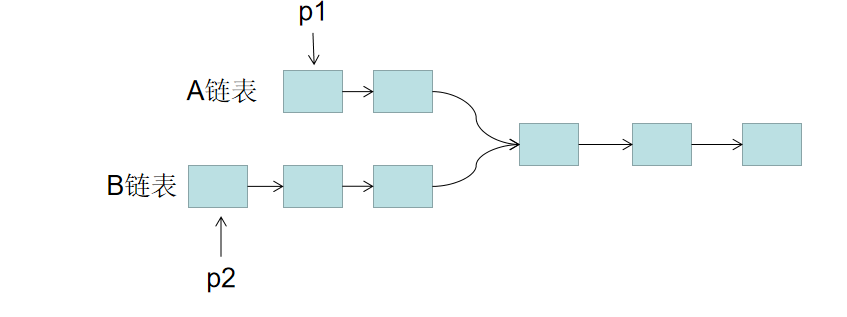
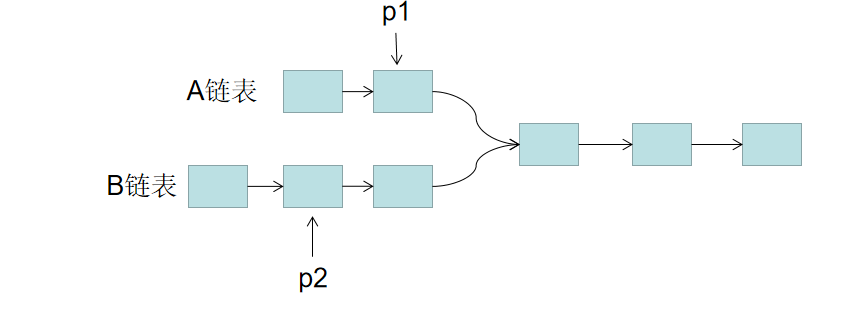
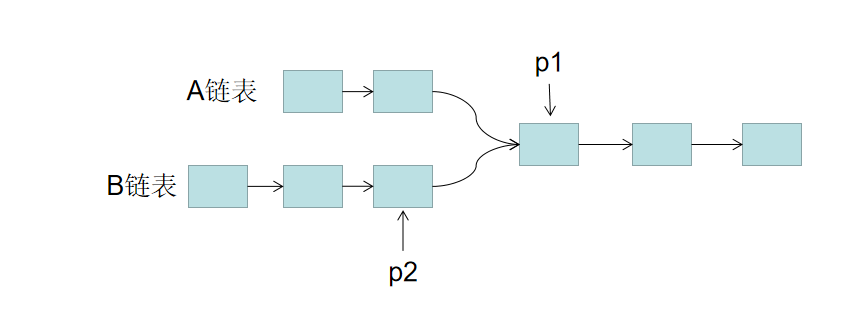
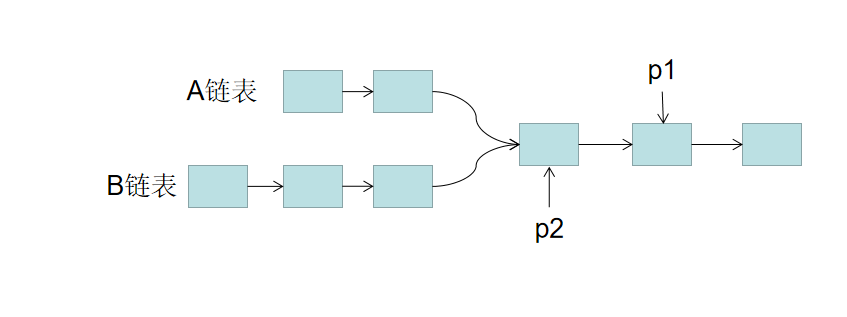
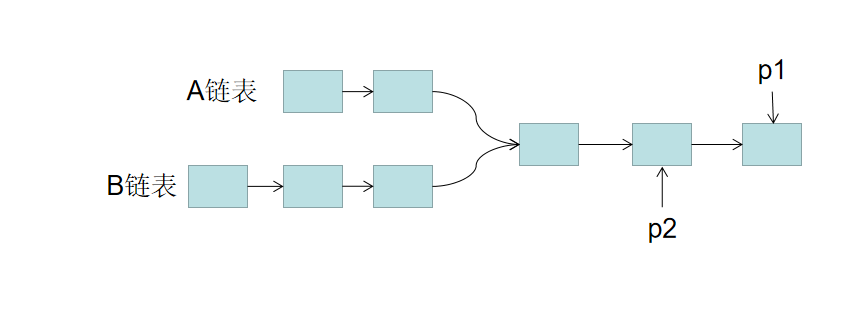
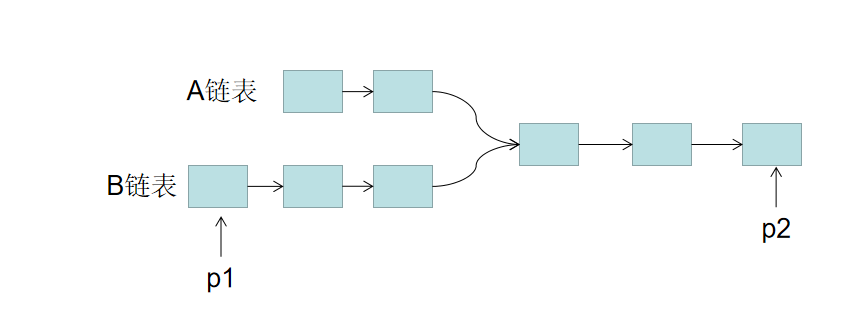
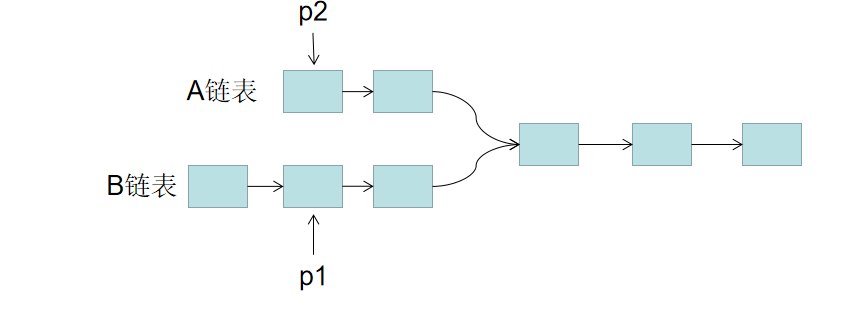
思路: 1. 用两个指针 p1,p2 分别指向两个链表 headA,headB 的头结点,同时向后遍历。
解释
A链表总长度为LA + C,B链表总长度为LB + C。
class Solution {public : ListNode *getIntersectionNode (ListNode *headA, ListNode *headB) { auto p = headA, q = headB; while (p != q) { if (p) p = p->next; else p = headB; if (q) q = q->next; else q = headA; } return p; } };
假设链表为 1→2→3→∅,我们想要把它改成 ∅←1←2←3。
在遍历链表时,将当前节点的 next 指针改为指向前一个节点。由于节点没有引用其前一个节点,因此必须事先存储其前一个节点。在更改引用之前,还需要存储后一个节点。最后返回新的头引用。
class Solution {public : ListNode* reverseList (ListNode* head) { ListNode* prev = nullptr ; ListNode* cur = head; while (cur) { ListNode* next = cur->next; cur->next = prev; prev = cur; cur = next; } return prev; } };
题意:给定一个链表要求判断链表节点是否构成回文链表
思路:将链表节点依次加入数组中,将问题转化为判断数组是否是回文数组,时间复杂度
class Solution {public : bool isPalindrome (ListNode* head) vector<int > res; bool flag = true ; ListNode* cur = head; while (cur) { res.push_back (cur->val); cur = cur->next; } for (int i = 0 , j = res.size () -1 ; i < j; i ++, j --) { if (res[i] != res[j]) { flag = false ; break ; } } return flag; } };
思路二:快慢指针
避免使用 O(n) 额外空间的方法就是改变输入。
我们可以将链表的后半部分反转(修改链表结构),然后将前半部分和后半部分进行比较。比较完成后我们应该将链表恢复原样。虽然不需要恢复也能通过测试用例,但是使用该函数的人通常不希望链表结构被更改。
该方法虽然可以将空间复杂度降到 O(1),但是在并发环境下,该方法也有缺点。在并发环境下,函数运行时需要锁定其他线程或进程对链表的访问,因为在函数执行过程中链表会被修改。
算法
整个流程可以分为以下五个步骤:
找到前半部分链表的尾节点。
反转后半部分链表。
判断是否回文。
恢复链表。
返回结果。
执行步骤一,我们可以计算链表节点的数量,然后遍历链表找到前半部分的尾节点。
我们也可以使用快慢指针在一次遍历中找到:慢指针一次走一步,快指针一次走两步,快慢指针同时出发。当快指针移动到链表的末尾时,慢指针恰好到链表的中间。通过慢指针将链表分为两部分。
class Solution {public : ListNode* endOfFirstHalf (ListNode* head) { ListNode* fast = head; ListNode* slow = head; while (fast->next != nullptr && fast->next->next != nullptr ) { fast = fast->next->next; slow = slow->next; } return slow; } ListNode* reverseList (ListNode* head) { ListNode* prev = nullptr ; ListNode* cur = head; while (cur != nullptr ) { ListNode* nextTemp = cur->next; cur->next = prev; prev = cur; cur = nextTemp; } return prev; } bool isPalindrome (ListNode* head) if (head == nullptr ) return true ; ListNode* firstHalfEnd = endOfFirstHalf (head); ListNode* secondHalfEnd = reverseList (firstHalfEnd->next); ListNode* l = head; ListNode* r = secondHalfEnd; bool flag = true ; while (flag && r != nullptr ) { if (l->val != r->val) flag = false ; l = l->next; r = r->next; } return flag; } };
题意:链表是否存在环路
思路:双指针,定义快慢指针,快指针每次移动两个节点,慢指针每次移动一个节点,每次判断快慢指针指向节点的下一个节点是否相同即可。时间复杂度
class Solution {public : bool hasCycle (ListNode *head) if (head == nullptr ) return false ; ListNode* fast = head; ListNode* low = head; while (fast->next != nullptr && fast->next->next != nullptr ) { fast = fast->next->next; low = low->next; if (low-> next == fast->next) { return true ; } } return false ; } };
快慢指针相遇时 :当快慢指针相遇时,只能证明链表中有环,但相遇点不一定是环的入口节点。环的入口节点定位 :根据 Floyd 的算法,当快慢指针相遇后,将一个指针重新指向链表头部,然后两个指针以相同速度前进,再次相遇的点就是环的入口节点。
class Solution {public : ListNode *detectCycle (ListNode *head) { if (head == nullptr || head->next == nullptr ) { return nullptr ; } ListNode* fast = head; ListNode* slow = head; while (fast != nullptr && fast->next != nullptr ) { fast = fast->next->next; slow = slow->next; if (fast == slow) { ListNode* ptr = head; while (ptr != slow) { ptr = ptr->next; slow = slow->next; } return ptr; } } return nullptr ; } };
/** * Definition for singly-linked list. * struct ListNode { * int val; * ListNode *next; * ListNode() : val(0), next(nullptr) {} * ListNode(int x) : val(x), next(nullptr) {} * ListNode(int x, ListNode *next) : val(x), next(next) {} * }; */ class Solution { public: ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) { if(list1 == nullptr) { return list2; } else if(list2 == nullptr) { return list1; } else if(list1->val < list2->val) { list1->next = mergeTwoLists(list1->next, list2); return list1; } else { list2->next = mergeTwoLists(list2->next, list1); return list2; } } };
aaaaaaaaaaaaaa