考研算法全程训练营
第一周
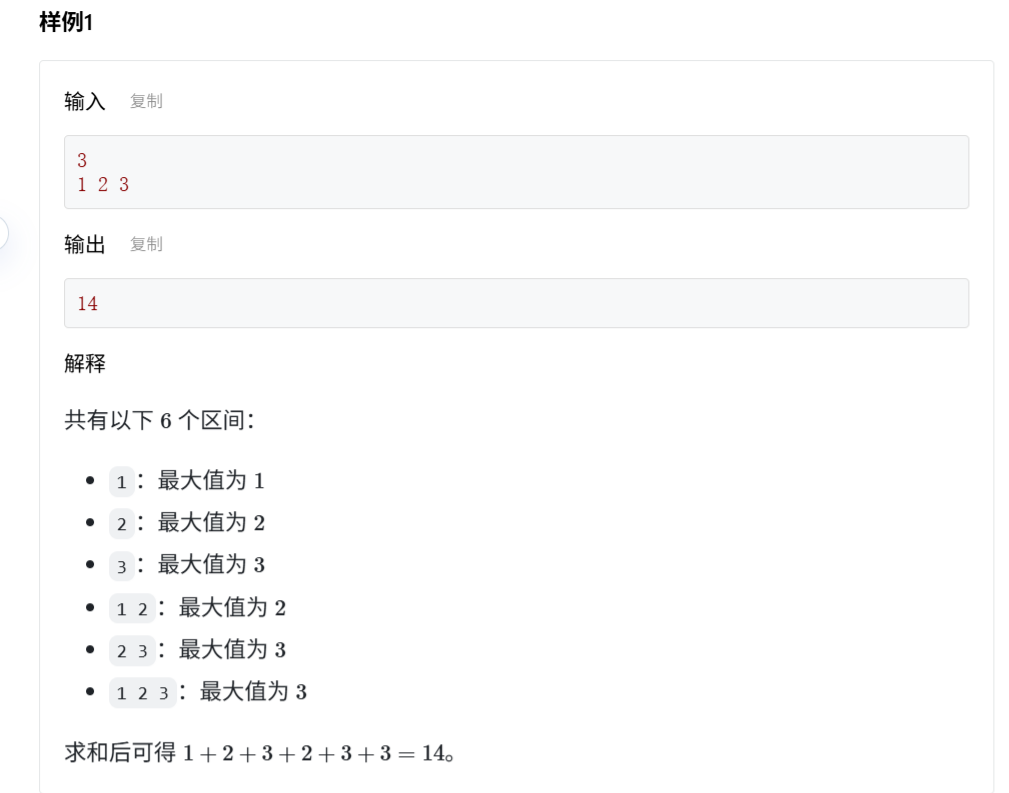
数组折叠求和
统计目标字符
题意：求第一个正数对应的下标
思路1：枚举，当读入到第一个正数输出输出对应下标 O(n)
思路2：二分查找第一个正数的下标，二分下标即可
枚举代码
#include <iostream> using namespace std; const int N = 1e5 + 10; int a[N]; int idx = -1; int n; int main() { scanf("%d", &n); for(int i = 0; i < n; i ++) { scanf("%d", &a[i]); if(a[i] > 0) { idx = i; break; } } if(idx == -1) { cout << -1 << endl; } else { cout << idx << endl; } return 0; }
二分代码：
#include <iostream> using namespace std;const int N = 1e5 + 10 ;int a[N];int idx = -1 ;int n;int main () scanf ("%d" , &n); for (int i = 0 ; i < n; i ++) { scanf ("%d" , &a[i]); } int l = 0 , r = n - 1 ; while (l < r) { int mid = l + r >> 1 ; if (a[mid] > 0 ) r = mid; else l = mid + 1 ; } if (l == n - 1 && a[l] < 0 ) cout << -1 << endl; else cout << l << endl; return 0 ; }
题意：根据题目给出的数组，交替输出最大最小值
思路：排序后，双指针i j分别指向最大最小值进行输出
#include <iostream> #include <algorithm> using namespace std;const int N = 1e5 + 10 ;int a[N];int n;int main () cin >> n; for (int i = 0 ; i < n; i ++) { cin >> a[i]; } sort (a, a + n); for (int i = 0 , j = n - 1 ; i <= j; i ++, j --) { if (i != j) cout << a[j] << " " << a[i] << " \n" [j - i == 1 ]; else cout << a[i]; } return 0 ; }
第二周
题意如题
思路；前缀和，将整数全赋值1，
负数为0，那么区间和就表示区间正整数的数量
#include <iostream> using namespace std;typedef long long LL;const int N = 1e5 + 10 ;LL a[N]; int n, m;int main () cin >> n; for (int i = 1 ; i <= n; i ++) { cin >> a[i]; a[i] = (a[i] > 0 ? 1 : 0 ); a[i] += a[i - 1 ]; } cin >> m; while (m --) { int l, r; cin >> l >> r; l ++, r ++; cout << a[r] - a[l - 1 ] << endl; } return 0 ; }
题意：
思路：贪心，先用面额大的
#include <iostream> using namespace std;int x, y;int main () cin >> x >> y; y -= x; int a, b, c; c = y / 5 ; y %= 5 ; b = y / 2 ; y %= 2 ; a = y; cout << a << ' ' << b << ' ' << c << endl; return 0 ; }
奇偶消消栈
#include <iostream> #include <vector> #include <cstdlib> using namespace std;int main () int n; cin >> n; vector<int > st; while (n--) { int x; cin >> x; st.push_back (x); while (st.size () >= 2 ) { auto u = st.back (); st.pop_back (); auto v = st.back (); st.pop_back (); if (u % 2 == v % 2 ) { st.push_back (abs (u - v)); } else { st.push_back (v); st.push_back (u); break ; } } } int sum = 0 ; for (auto val : st) { sum += val; } cout << sum << "\n" ; return 0 ; }
题意：
思路：循环队列，res存放队列和，每次入队后判断队列和res是否大于k，大于则队头出队，折半入队，res也需要动态修改。
#include <bits/stdc++.h> using namespace std;typedef long long LL;queue<int > q; int n, k;LL res; int main () ios::sync_with_stdio (0 ), cin.tie (0 ), cout.tie (0 ); cin >> n >> k; for (int i = 1 ; i <= n; i ++) { int x; cin >> x; q.push (x); res += x; while (res > k) { int t = q.front (); q.pop (); res -= t; t /= 2 ; q.push (t); res += t; } } while (q.size ()) { cout << q.front () << " \n" [q.size () == 1 ]; q.pop (); } return 0 ; }
第三周
题意：找到链表最大值，并在最大的节点后插入一个最大的节点
思路：遍历两次链表，第一次找最大值，第二次遍历，遍历到最大值节点，进行插入
void insertAfterMaxData (ListNode* head) ListNode* currentNode = head->next; int maxVal = head->next->val; while (currentNode != nullptr ) { if (maxVal < currentNode->val) { maxVal = currentNode->val; } currentNode = currentNode->next; } currentNode = head->next; while (currentNode != nullptr ) { if (maxVal == currentNode->val) { ListNode* newNode = new ListNode (maxVal); newNode->next = currentNode->next; currentNode->next = newNode; currentNode = newNode->next; } else { currentNode = currentNode->next; } } }
题意：
思路：
#include <bits/stdc++.h> using namespace std; string s; string OP(string &s) { int n = s.size(); if(n < 2) { return s; } int midIdx = n / 2; string l, r, mid = ""; if(n % 2 == 0) { l = s.substr(0, midIdx); r = s.substr(midIdx, n - midIdx); } else { l = s.substr(0, midIdx); mid = s[midIdx]; r = s.substr(midIdx + 1, n - midIdx - 1); } string lRes = OP(l); string rRes = OP(r); if(lRes < rRes) { swap(lRes, rRes); } return lRes + mid + rRes; } int main() { ios::sync_with_stdio(0), cin.tie(0), cout.tie(0); cin >> s; // OP(s); s = OP(s); cout << s << "\n"; return 0; }
题意：
思路：
#include <bits/stdc++.h> using namespace std;typedef long long LL;LL n, m; LL S (LL n, LL m, LL k) return n + k * m - (k * (k + 1 )) / 2 ; } int main () cin >> n >> m; LL l = 1 , r = 2000000000 ; while (l < r) { LL mid = (l + r) / 2 ; if (S (n, m, mid) <= 0 ) { r = mid; } else { l = mid + 1 ; } } cout << l << "\n" ; return 0 ; }
题意：给定两个字符串 A 和 B，判断是否可以通过从 A 中删除若干字符得到
B。如果可以，输出被删除的字符（按 A 中原顺序）；否则输出
NO_RESULT。数据保证答案唯一。
思路：双指针
#include <bits/stdc++.h> using namespace std;string str1, str2, res; int main () cin >> str1 >> str2; int i, j; for (i = 0 , j = 0 ; i < str1. size () && j < str2. size (); i ++) { if (str1[i] == str2[j]) j ++; else res += str1[i]; } if (j == str2. size ()) { for (; i < str1. size (); i ++) { res += str1[i]; } cout << res << "\n" ; } else { cout << "NO_RESULT\n" ; } return 0 ; }
第四周
题意：
思路：贪心，每次将数组最大和最小配对，所有都符合条件即成功
#include <bits/stdc++.h> using namespace std;vector<int > a, b; int n, x;bool flag = true ;int main () cin >> n >> x; for (int i = 0 ; i < n; i ++) { int number; cin >> number; a.push_back (number); } for (int i = 0 ; i < n; i ++) { int number; cin >> number; b.push_back (number); } sort (a.begin (), a.end ()); sort (b.begin (), b.end (), greater <int >()); for (int i = 0 ; i < n; i ++) { if (a[i] + b[i] > x) { flag = false ; break ; } } cout << (flag ? "Yes" :"No" ) << "\n" ; return 0 ; }
第七周
题意：输出长度为n的串的所有可能结果，每一位只能是0、1、2
思路：DFS
#include <bits/stdc++.h> using namespace std;const int N = 20 ;int path[N];bool st[N][N];int n;void dfs (int u) if (u > n) { for (int i = 1 ; i <= n; i ++) cout << path[i]; cout << "\n" ; return ; } for (int i = 0 ; i <= 2 ; i ++) { if (!st[u][i]) { st[u][i] = true ; path[u] = i; dfs (u + 1 ); path[u] = 0 ; st[u][i] = false ; } } } int main () ios::sync_with_stdio (0 ), cin.tie (0 ), cout.tie (0 ); cin >> n; dfs (1 ); return 0 ; }
第十周
题意：给出书的根节点，判断是否是完全二叉树
思路：BFS
bool isCompleteTree (TreeNode* root) queue<TreeNode *> q; q.push (root); bool foundNullptr = false ; while (q.size ()) { auto t = q.front (); q.pop (); if (t == nullptr ) { foundNullptr = true ; } else { if (foundNullptr) return false ; q.push (t -> left); q.push (t -> right); } } return true ; }
第十一周
题目：给定一个邻接表表示的图，求度最大的顶点
思路：邻接表图，出度即为节点行不唯一的数，入度为列不唯一的数量
int findMaxDegreeVertex (int ** G, int n) int res = 0 , max_degree = 0 ; for (int i = 0 ; i < n; i ++) { int d = 0 ; for (int j = 0 ; j < n; j ++) d += G[i][j] + G[j][i]; if (d > max_degree) { max_degree = d; res = i; } } return res; }
int countTwinConnectedComponents (int ** G, int n) vector<int > degree (n) ; for (int i = 0 ; i < n; i ++) { degree[i] = 0 ; for (int j = 0 ; j < n; j ++) { degree[i] += G[i][j]; } } int twinCount = 0 ; for (int i = 0 ; i < n; i ++) { if (degree[i] == 1 ) { for (int j = i + 1 ; j < n; j ++) { if (G[i][j] == 1 && degree[j] == 1 ) { twinCount ++; } } } } return twinCount; }
思路：
void DFS (int u, int **G, vector<bool > &visited, int n, int &count) visited[u] = true ; count ++; for (int v = 0 ; v < n; v ++) { if (G[u][v] == 1 && !visited[v]) { DFS (v, G, visited, n, count); } } } int largestConnectedComponent (int ** G, int n) vector<bool > visited (n, false ) ; int maxCount = 0 ; for (int i = 0 ; i < n; i ++) { if (!visited[i]) { int count = 0 ; DFS (i, G, visited, n, count); if (count > maxCount) { maxCount = count; } } } return maxCount; }
题意：给定顶点，计算每层节点的数量
思路：DFS 定义visited
布尔数组。记录每个顶点是否背访问过，首先将起点加入队列，
并将visited标记为true，广度优先每次所含节点即为当前层的节点数
vector<int > countLevel (int ** G, int n, int s) { vector<bool > visited (n, false ) ; vector<int > res; queue<int > q; visited[s] = true ; q.push (s); while (q.size ()) { int levelSize = (int )q.size (); res.push_back (levelSize); for (int i = 0 ; i < levelSize; i ++) { int u = q.front (); q.pop (); for (int v = 0 ; v < n; v ++) { if (G[u][v] == 1 && !visited[v]) { visited[v] = true ; q.push (v); } } } } return res; }
wechat
alipay
